¡¡¡¡¡Qué locura es conocer a estos números!!!!!!!,

Mira las maravillas de estos numeros

VIDEOS DE

LOS NÚMEROS DEL 1 al 9

¿Dónde te encuentro?

El siete es un número misterioso y mágico. Muchos aspectos de la vida del hombre son regidos por este número. Son siete días los que tiene la semana, los mismos que ocupó dios para formar la tierra. Son siete los mares del planeta. Los indús han descubierto siete chacras o puntos de energía en el cuerpo, siete maravillas del mundo, siete pecados capitales, siete calamidades. Dante describe siete infiernos, los metafísicos hablan de siete niveles de conciencia, Blanca Nieves se acompaña por siete enanos, el arco iris tiene siete colores, son siete las notas musicales, las botas de siete leguas, siete vidas tiene un gato y la serpiente de siete cabezas, entre otras muchas.


Siete proviene del latín séptem, séptimo. De acuerdo a la Real Academia Española, es un signo o conjunto de signos con que se presenta el número siete. Buscando el origen de este número, observamos que los primeros sistemas reales de numeración que conocemos pertenecen a egipcios y sumerios. Lo egipcios adoptaron el 10 como base para su numeración, partiendo de que la mano tiene cinco dedos y las dos manos 10. En tanto que los sumerios se circunscribieron a un sistema sexagesimal; es decir, de base 60. Sesenta constituía la primera gran unidad y sesenta veces sesenta (3,600) fue por mucho tiempo el número más allá  del cual no se concebía  pudiera haber más números, y de aquí su nombre de sar(círculo, totalidad)

De acuerdo a esta interpretación griega de los números, el siete es la unidad universal. Tiene un parentesco con el cuatro, símbolo de la tierra, que representa la realización de la unidad del mundo. Esta semejanza hace que al siete se le atribuyan  los siete astros errantes o planetas (Mercurio, Venus, Marte, Júpiter, Saturno, luna, sol). Cuando procede del 6+1 se representa por una estrella de seis puntas con un punto en su centro, es el equilibrio tendiendo a la interioridad, revelando el misterio de la circulación de las fuerzas de la naturaleza.

 En la cultura judía el número siete desempeña un papel fundamental en la fonética y es el que domina el ciclo del año. Cada séptimo días es su sabbat; el séptimo mes es sagrado; el séptimo año es un año sabático. El año del jubileo era determinado por el número siete, multiplicado por siete. La fiesta de los Azimos (pan) duraba siete días, lo mismo la festividad de la Pascua judía. También se habla de los siete frutos de Israel, siete cielos, siete cámaras del paraíso; siete categorías de las almas judías, los siete pastores de Israel (Abraham, Isaac, Yaacob, Moisés, Aarón, David y Salomón). En la antigüedad se determinaba que las Curadoras debían cumplir ciertas condiciones. Ser la séptima hija de una séptima hija o el séptimo hijo de un séptimo hijo, se dice que daba poder de curar por medio del tacto. Se aceptaba el siete como el más sagrado de los números y los séptimos hijos poseían “doble vista” y el arte de ver el futuro. Esta tradición se fue perdiendo con el tiempo, a medida que las familias dejaban de ser tan numerosas. Todavía en la época victoriana se usaba como tradición, en familias numerosas, que el séptimo hijo cursara la carrera de medicina. A estos hijos se les conocía como el Hijo Septimus.

Lo curioso de esto es que estas concepciones míticas del siete también la encontramos en otras culturas precolombinas de América Latina. Entre los aztecas  siempre aparece el número siete, número también sagrado para estas civilizaciones, contándose el Templo Siete Mazorcas, relacionado con el Maíz, alimento principal en estos pueblos.

Mucho de la magia o encanto por el siete, probablemente deviene por el interés que despertó en los primeros hombres los fenómenos del cielo. Su curiosidad les permitió observar desde la tierra, los ciclos repetitivos de los objetos celestes. Esta observación del movimiento de los planetas fue una herramienta ideal para la medición del paso del tiempo. Así pudieron determinar los meses y los días. Y aunque algunos atribuyen un origen bíblico a la duración de la semana de siete días, tiempo según la tradición judeo-cristiana, que le llevó a Dios la creación del mundo. Sin embargo, parece ser que la observación del cielo fue la que fijó la duración de las semanas. Y es que son siete los cuerpos celestes –visibles a simple vista- fácilmente identificables por describir movimientos diferentes a las estrellas. Estos cuerpos, también llamados Vagabundos, son: el Sol, la Luna, Marte, Mercurio, Venus, Júpiter y Saturno. Es por ello que sus nombres guardan relación con los días de la semana. Domingo, dedicado al sol, proviene del latín dies solis, día del sol. Lunes; dies lunae, día de la Luna. Martes; dies martis, día de Marte. Miércoles; dies mercurii, día de Mercurio. Jueves; dies jovis, día de Júpiter. Viernes; dies veneris, día de Venus. Sábado; dies saturni, día de Saturno.

Platón escribió al respecto en sus Diálogos que el Sol y la Luna y las otras cinco estrellas llamadas planetas fueron creadas por el (dios) para distinguir y preservar los “Números del Tiempo”.

Existen muchos otros misterios y mitos alrededor del número siete. Las Siete Trompetas que anuncian el juicio de Dios sobre Roma, las Siete Copas de la Ira, así como las Siete Plagas Postreras que anuncian el Apocalipsis, son entre otras, parte de la gracia, misterio, encanto, magia o fascinación que ejerce este número en nuestras vidas y otras, como los siete colores del arco iris, las siete notas musicales y los siete mares, tal vez sean coincidencias o parte de los misterios de la humanidad.

Generalizando la Sección de Números Metálicos. Número mórficos: Oro y Plástico

Como ya se vio en las partes 1, 2 y 3, en arquitectura las proporciones son importantes y desde hace mucho tiempo los arquitectos se preguntan qué relaciones entre los tamaños de los distintos elementos arquitectónicos son las más apropiadas, es decir las más placenteras estética o funcionalmente. No en vano Goethe definió la arquitectura como música congelada. 

¿Cuáles son las proporciones ideales para las representaciones gráficas? ¿Existe una relación idónea entre el alto y ancho de una visualización?. 

Durante los últimos siglos se ha venido considerando que el número Fi, también llamado divina proporción o razón áurea, era un baremo de equilibrio y belleza en cuanto lo que a proporciones se refiere. El número Fi es 1.618033988..., que es el límite al que tiende la división entre dos números cualesquiera de la serie de Fibonacci, 

La serie de Fibonacci se construye muy fácilmente, cada término es la suma de los dos anteriores, empezando por 0 y 1:

0  1  1  2  3  5  8  13  21  34  55  89  144  233 ...

La gracia de la razón áurea es que es una proporción que se encuentra con cierta frecuencia en la naturaleza, especialmente en la geometría, pero también en las proporciones aproximadas del cuerpo humano.

De ello hay muchos ejemplos interesantes en la web de Ron Knotts de la Universidad de Surrey  o (en este caso bastante más discutibles) en Goldennumber.net. Pero también hay muchos errores de concepto alrededor de Fi. 

Por ejemplo es un error común pensar que en el caparazón del Nautilus, un cefalópodo marino, Fi juega un papel importante. Esto no es así, su caparazón es una espiral logarítmica no una espiral áurea, como se puede ver en "Spirals and the Golden Section" de John Sharp. Muchas atribuciones de proporciones áureas a fenómenos naturales son sólo aproximaciones voluntaristas.

Pero volvamos a nuestro interés, el número Fi es un representante de los denominados números mórficos que tienen la interesante propiedad de que existen dos valores k y l para los que se cumple que

Condición de número mórfico. k=2 y l=1 dan la razón áurea, k=3 y l=4, el número plástico. El gráfico muestra las interesantes propiedades de estos dos número. Si p es la razón áurea, 1+p=p2 y p-1=1/p. Si p es el número plástico se cumple p-1= p-4 y p3=p+1.

En seguida nos preguntamos ¿existe algún número mórfico aparte de la sección áurea?. Arts Fokkink y Kruijtzer de la Universidad de Delft demuestran en su artículo “Morphic numbers” que sólo existen dos números mórficos: la sección áurea y el número plástico (1,3247179...), descubierto en 1928 por el arquitecto y monje benedictino Hans van der Laan, que lo utilizó como base para sus construcciones arquitectónicas. El número plástico da lugar a la escala de Van der Laan que sirvió de base para la construcción de la capilla de St. Benedictusberg, abadía benedictina.

Interior de la capilla de la abadía de Sint Benedictusberg, diseñada por Hans van der Laan(1904-1991) usando el número plástico como la base para su escala. Pulse sobre la imagen para agrandarla

Respondiendo a nuestra pregunta, ¿podrían ser la sección áurea o el número plástico la proporción ideal para realizar representaciones gráficas?. No hay ningún indicio irrefutable que así lo indique. Sir William Playfair reputado como uno de los primeros en usar gráficos de barras en el siglo 18, usó predominantemente valores próximos a la sección áurea para proporcionar sus gráficos, aunque también hizo uso de otras proporciones.

Edward Tufte apunta que las preferencias visuales por las proporciones en las formas rectangulares se han venido estudiando desde 1860 por parte de los sicólogos encontrando una suave preferencia por las proporciones alrededor de la sección áurea pero con una variación que va desde 1, 2 hasta 2,2.

La existencia de una proporción “natural” que conectase con las raíces preceptivas de la especie humana no es un despropósito. De existir proporcionaría una base sobre la que construir escalas armoniosas y gráficos probablemente menos engorrosos de manejar. Una idea relacionada es la de que, dada la naturaleza fractal del mundo, la visualización de la información en forma fractal quizá sea más próxima a la manera natural de captar el mundo y por tanto pueda ser ventajosa.

Aunque la idea es muy atractiva, lamentablemente no se encuentran evidencias irrefutables de ello. La forma en que procesamos la información perceptiva los seres humanos es en gran parte un misterio todavía. Los estructuralistas consideran por ejemplo que todas las representaciones son arbitrario-convencionales, negando la posibilidad de que haya representaciones sensoriales, innatas, comprensibles sin necesidad de aprendizaje. Otra gente piensa de muy distinta manera...

Frente a esta situación se impone el pragmatismo. Siguiendo a Tufte, si la naturaleza de la representación sugiere su propia forma, síguela. Si no, usa preferentemente una proporción más ancha que alta con una proporción que te parezca útil o satisfactoria. 

En mi opinión personal, el uso consistente de una escala coherente, sea la sección áurea, la escala de Van der Laan o cualquier otra proporción es una buena elección para construir representaciones armoniosas. 

LOS NÚMEROS METÁLICOS. 3º PARTE

Sucesión de Fibonacci

Gráfica de la sucesión de Fibonacci hasta f₁₀

En matemáticas, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales:

El primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores:

A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación,matemáticas y teoría de juegos.

Los números de Fibonacci  quedan definidos por las ecuaciones

(1)

(2)

(3) para 

Esto produce los números

• 
• 
• 
• 
• 
• 
• 
• 
• 

y así sucesivamente hasta el infinito.

Propiedades de la sucesión

Al construir bloques cuya longitud de lado sean números de Fibonacci se obtiene un dibujo que asemeja al rectángulo áureo (véaseNúmero áureo).

Los números de Fibonacci aparecen en numerosas aplicaciones de diferentes áreas. Por ejemplo, en modelos de la crianza de conejos o de plantas, al contar el número de cadenas de bits de longitud n que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes. De hecho, existe una publicación especializada llamada Fibonacci Quarterly⁴ dedicada al estudio de la sucesión de Fibonacci y temas afines. Se trata de un tributo a cuán ampliamente los números de Fibonacci aparecen en matemáticas y sus aplicaciones en otras áreas. Algunas de las propiedades de esta sucesión son las siguientes:

• La razón o cociente entre un término y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo. Es decir:

Este límite no es privativo de la Sucesión de Fibonacci. Cualquier sucesión recurrente de orden 2, como la sucesión 3, 4, 7, 11, 18,..., lleva al mismo límite. Esto fue demostrado por Barr y Schooling en una carta publicada en la revista londinense "The Field" del 14 de diciembre de 1912. Los cocientes son oscilantes; es decir, que un cociente es menor al límite y el siguiente es mayor. Los cocientes pueden ordenarse en dos sucesiones que se aproximan asintóticamente por exceso y por defecto al valor límite.

• Cada número de Fibonacci es el promedio del término que se encuentra dos posiciones antes y el término que se encuentra una posición después. Es decir

• La suma de los n primeros números es igual al número que ocupa la posición n + 2 menos uno. Es decir

Phi forma parte de una expresión de la sucesión de Fibonacci.

• El máximo común divisor de dos números de Fibonacci es otro número de Fibonacci. Más específicamente

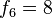
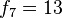
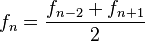
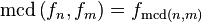
Esto significa que  y 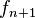 son primos relativos y que  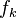divide exactamente a 

LOS NUMEROS METÁLICOS. 2º PARTE

Los números metálicos aparecen desde los sistemas usados en el diseño de las construcciones por la civilización romana hasta los más recientes trabajos de caracterización de caminos universales al caos.

Pero... ¿cómo se construyen estos números?. Todos sabemos que el número de oro φ=(1+√5)/2, es la raíz positiva de la ecuación x²-x-1=0. ¿Y qué nos impide generalizar un poco esta ecuación? Nada!. De hecho, podemos considerar la nueva ecuación x²-mx-1=0, donde m es un número natural. Todas las raíces positivas de estas ecuaciones son números metálicos:

• Si m=1, obtenemos φ, el número de oro.
• Si m=2, obtenemos σ_ag:=1+√2, el número de plata
• Si m=3, obtenemos σ_br:=(3+√13)/2, el número de bronce
• En general, se obtiene una sucesión σ_m:=(m+√m²+4)/2
  

Todos estos números σ_m tienen varias propiedades en común. Por supuesto, son todos irracionales cuadráticos y su representación en fracciones continuas es de lo más simple: σ_m:=[m], es decir,

¿Cómo se prueba esto? pues es muy sencillo. Partamos de la ecuación  x²-mx-1=0, y quedémosnos con el término cuadrático en el primer miembro, es decir, x²=mx+1. Si ahora dividimos ambos miembros entre x, resulta que x=m+1/x. Ahora basta con sustituir la x del denominador, por el valor de x que tenemos despejado. Pero esto es un proceso infinito que produce una fracción continua infinita y periódica.

Pero aún podemos dar más propiedades, esta vez, geométricas. Todos sabemos de la existencia del Rectángulo de Oro, como aquél cuyos lados guardan la relación 1:φ, es decir, el cociente del lado mayor entre el lado menor es, exactamente, φ. Este rectángulo tiene la propiedad que, si quitamos un cuadrado de lado 1 (o de lado igual al lado menor) de dentro del rectángulo, el  mini-rectángulo que queda es proporcional al original, es decir, sus nuevos lados guardan las mismas proporciones que el original. Compruébalo en la siguiente imagen:
De forma análoga, podemos construir el rectángulo de plata con proporciones 1:σ _ag. En este caso, si del rectángulo original quitamos 2 cuadrados de lado 1, el mini-rectánguloque resulta es semejante al original, como se puede comprobar en el dibujo siguiente:
En general, podemos construir el emésimo rectángulo metálico con proporciones 1:σ_m y de forma que si eliminamos m cuadrados de lado 1, el mini-rectángulo que resulta es semejante al original

LA FAMILIA DE NUMEROS METALICOS. 1º PARTE

El Número de Oro

      En nuestra búsqueda permanente por relacionar los contenidos matemáticos con otras áreas, pensé que podría interesarles interiorizarnos acerca del origen y uso del número de oro, tan valorado por incontables artistas que han recurrido a él para ajustar las proporciones de sus obras. 

    Tanto en arquitectura como en el Arte, las personas se han preguntado desde siempre cuáles son las proporciones que hacen que una obra sea más armónica a la vista. Tomando el rectángulo como una de las figuras que se encuentra con mayor frecuencia en construcciones (fachadas de edificios, puertas, ventanas, cuadros, espejos, etc.), nos preguntamos: ¿qué relación debe haber entre la base y la altura de esta figura para que sea lo más armoniosa posible a la vista?


      Si bien el gusto es subjetivo, basándonos en la opinión de los griegos de la época clásica vamos a estudiar el rectángulo áureo, al cual ellos consideraban el más proporcionado.

Rectángulo áureo:

      Es aquel que posee una propiedad curiosa: si se le quita un cuadrado -el mayor posible- se obtiene otro rectángulo semejante al primero.

      Si tomamos como unidad el lado menor, podemos calcular la medida del mayor. Debe cumplir la siguiente proporción:

Solución: 

es la llamada razón áurea; número de oro o número de Fidias, llamado también así dado que fue él quien lo empleó para diseñar El Partenón.

El número de oro: 

     Es una de las dos raíces de la ecuación , cuyo valor decimal habitualmente utilizado es 1,618.


      Se lo suele encontrar en las pirámides de Egipto, en la arquitectura griega, en las obras de Rafael, Leonardo da Vinci, etc. Este número está lleno de recursos; pueden darse de él múltiples representaciones; es apto para representar múltiples fenómenos. Era conocido por los pitagóricos -quienes lo consideraban un número místico- por ser la razón entre la diagonal y el lado del pentágono regular, figura transcendente para ellos. Este pentágono, también llamado "triple triángulo", era la insignia de los pitagóricos.

      El número de oro forma parte de un conjunto de números especiales llamados números metálicos. Algunos de ellos son:

Número de plata: 

Número de bronce: 

Construcción del rectángulo áureo:

      Para realizar esta construcción, necesitaremos regla y compás. Procederemos de la siguiente manera:


1°) Construimos un cuadrado de lado a

2°) Dividimos el cuadrado en dos rectángulos iguales:

3°) Trazamos la diagonal del segundo rectángulo y marcamos dicha medida sobre la horizontal:

4°) Queda así determinado la base de un rectángulo áureo, que tiene como altura el lado del cuadrado:

      Vamos a comprobar que realmente se trata de un rectángulo áureo. Para ello, debemos dividir su base por su altura: si el número que resulte de esta operación es el número de oro, habremos logrado nuestro objetivo.


Calculamos el valor de d: (utilizaremos el teorema de Pitágoras)

Por lo tanto: 

Calculamos el valor de la base:

Por lo tanto: 

Calculamos la razón entre la base y la altura del rectángulo:

Por lo tanto: