Sucesión de Fibonacci
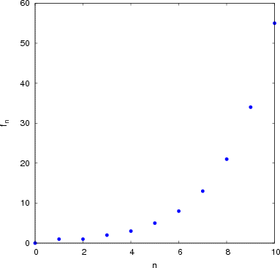
El primer elemento es 0, el segundo es 1 y cada elemento restante es la suma de los dos anteriores:
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación,matemáticas y teoría de juegos.
Los números de Fibonacci  quedan definidos por las ecuaciones
quedan definidos por las ecuaciones
 quedan definidos por las ecuaciones
quedan definidos por las ecuacionesEsto produce los números
y así sucesivamente hasta el infinito.
Propiedades de la sucesión
Los números de Fibonacci aparecen en numerosas aplicaciones de diferentes áreas. Por ejemplo, en modelos de la crianza de conejos o de plantas, al contar el número de cadenas de bits de longitud n que no tienen ceros consecutivos y en una vasta cantidad de contextos diferentes. De hecho, existe una publicación especializada llamada Fibonacci Quarterly4 dedicada al estudio de la sucesión de Fibonacci y temas afines. Se trata de un tributo a cuán ampliamente los números de Fibonacci aparecen en matemáticas y sus aplicaciones en otras áreas. Algunas de las propiedades de esta sucesión son las siguientes:
- La razón o cociente entre un término y el inmediatamente anterior varía continuamente, pero se estabiliza en el número áureo. Es decir:
- Este límite no es privativo de la Sucesión de Fibonacci. Cualquier sucesión recurrente de orden 2, como la sucesión 3, 4, 7, 11, 18,..., lleva al mismo límite. Esto fue demostrado por Barr y Schooling en una carta publicada en la revista londinense "The Field" del 14 de diciembre de 1912. Los cocientes son oscilantes; es decir, que un cociente es menor al límite y el siguiente es mayor. Los cocientes pueden ordenarse en dos sucesiones que se aproximan asintóticamente por exceso y por defecto al valor límite.
- Cada número de Fibonacci es el promedio del término que se encuentra dos posiciones antes y el término que se encuentra una posición después. Es decir
- La suma de los n primeros números es igual al número que ocupa la posición n + 2 menos uno. Es decir
- El máximo común divisor de dos números de Fibonacci es otro número de Fibonacci. Más específicamente
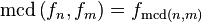
- Esto significa que
 y
y 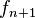 son primos relativos y que
son primos relativos y que 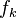 divide exactamente a
divide exactamente a 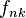






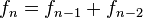 para
para 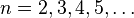




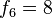
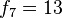


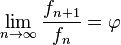
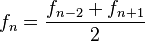

Me encantaría ver una demostración de algunas propiedades que se han colocado aquí. Por ejemplo la del máximo común divisor entre dos números de fibonacci. Estaría muy bueno!. ¿Quien la hizo?. Alguien se anima a demostrar lo que se sugiere en este Blog?.
ResponderEliminarHe visto que mucha información es sacada de Wikipedia. Parece que eres un aficionado de esa página. ¿me equivoco?.